| |
optometry formulas |
| |
When an ECP prescribes a certain prescription, he is really specifying the focal power "on-axis" which is made by the optician in the form of surface power of ophthalmic lens. The lens so made either converges or diverges the bundle of rays. Vergence determines the direction and power of light transmission by the lens.
• Focal Power : Expresses the focal length of the lens.
• Vergence Power : Measures the lens ability to converge or diverge the bundle of light rays.
• Surface Power : Algebraic summation of the powers of Cx and CC surfaces gives the approximate focal power of the lens. Algebraic summation of the powers of Cx and CC surfaces gives the approximate focal power of the lens.
|
| |
Focal Power of the
Ophthalmic Lens |
Vergence Power of the Ophthalmic Lens |
Surface Power of the
Ophthalmic Lens |
|
Light bending ability of the lens is denoted by the focal power of the lens, expressed in “Dioptre” and is denoted by “D”.
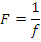
Where F = Focal Power in Dioptre
f = Focal Length of the lens in metres
Application:
What is the focal length of a lens with a power of – 4.00D?
F = 1 / f
Or, -4.00 = 1 / f
Or, f = 1 / -4.00
Or, f = - 0.25 m
The focal length of a lens is + 33.33 cms. What is its power?
F = 1 / f
Or, F = 1 / 0.3333
Or, F = + 3.00 D |
Vergence can be understood as a measure of the curvature of the optical wavefront, expressed in “dioptre”. The vergence of light is defined by –
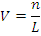
Where n = Refractive index of the lens material.
L = Distance in accordance with the Cartesian Sign Convention.
For light propagating away from a source.i.e,diverging, the vergence is negative i.e.
V = -n/L
For light propagating towards a focus’i.e, converging, the vergence is positive i.e.
V = +n/L |
Most ophthalmic lenses have two curved surfaces, with specific radius of curvature. The convex surface has always positive surface power and the concave surface has always negative surface power.
For example, if the Cx side surface power is + 6.00D and the CC side surface power is -8.00D, the focal power of the lens is -2.00D.
The surface power of the lens depends upon two factors:
1. Mean Radius of Curvature of the surface
2. Refractive Index of the lens material.
The surface power is denoted by F.
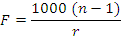
This may also be written as
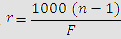
Where n is the refractive index of the lens material
r is the radius of the curvature in mm
Application:
A lens of refractive index 1.50 has a radius of curvature of -4.00 cms. What is the power of the lens surface in air?
Using the Lens Surface Power Formula
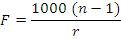
Or, F = 1000 (1.5 – 1 ) / -40
Or, F = 1000(0.5) / -40
Or, F = 500 / -40
Or, F = -12.50 D is the power of lens surface in air
|
|
| |
Prisms are mainly of two types - Refracting and Ophthalmic. Ophthalmic prisms are worked in ophthalmic lenses for correction of binocular vision disorder. Prism can be created on a spectacle lens by either decentration or by working prism on the lens during lens surfacing by working the surface of a prism lens with the surface of the optical lens using special tools.
Prism by Decentration: The lens is decentered using Prentice Rule.
Worked Prism: Prism is created while lens surfacing when a lens blank size is smaller. |
| |
Prism by Decentration |
Worked Prism |
Prentice Rule states that there is a relationship between the magnitude of prism, the power of the lens, and how much the lens is decentred from the optical centre of the lens.
P = cF
Where P = Prism power in Dioptres Δ
c = Decentration in cms
F = Lens power in Dioptres, D
Application
3Δ dioptres of prism needs to be created by a -1.00Dsph lens. Calculate the amount by which the lens must be decentred.
P = cF
Or, 3Δ = c x 1
Or, 3/1 = c
Or, c = 3 cm
So the lens must be decentered by 3cms
|
Making the edge thickness of the uncut lens different has the effect of shifting the position of the optical centre.
On any prismatic lens there is a relationship between the thickness at the apex and the thickness at the base. During the lens manufacturing, the difference in edge thicknesses will be calculated and controlled over a specified diameter.
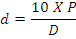
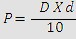
where, d = decentration in mm
D = dioptre or lens power
P = prism degree
The prism degree can be found out with the help of above equation and can be ground by keeping the edge difference for which the equation is:
Edge Difference. = Prism × size of lens × 0.019 |
|
| |
In practice, edge thickness is calculated for minus lenses and centre thickness is calculated for plus lens. An allowance is made for edge thickness in case of plus lens and for centre thickness for minus lenses. Sags are important to calculate the centre thickness of the plus lens and the edge thickness of the minus lens.
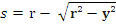
Where,
• s is Sag Value
• r is radius of curvature calculated from
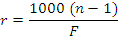
• y is the radius of the given lens
• n is the refractive index of the lens material
• F is the surface power of the lens |
| |
Centre Thickness of Plus Lenses |
Edge Thickness of Minus Lenses |
Since the sag denotes the centre thickness of plus lens, the expression for plus lens would be:
t = s + e
(where e denotes edge thickness)
Or, e = t – s
Application
A + 9.00 Dsph flat lens, made in 56 mm diameter and an edge thickness of 1 mm is made with a lens material having refractive index 1.523. What would be the centre thickness?
t = s + e
Where,
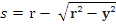
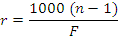
Putting the values to find r,
r = 1000(1.523-1)/9
Or, r = 1000(0.523)/9
Or, r = 523/9
Or, r = 58.11 mm.
Therefore, we have
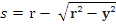
Or, s = 58.11 - √58.11² - 28²
Or, s = 58.11 - √3376.77 – 784
Or ,s = 58.11 - √2592.77
Or ,s = 58.11 – 50.92
Or, s = 7.19 mm.
Therefore,
t = s + e
Or, t = 7.19 + 1
Or ,t = 8.19 mm. |
Since the sag denotes the edge thickness of minus lens, the expression for minus lens would be:
e = s + t
(Where t denotes centre thickness)
Or, t = e – s
Application
A -12.00 Dsph flat lens, made in 52 mm diameter and a centre thickness of 2 mm
is made in crown glass. What would
be the edge thickness?
e = s + t
Where,
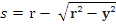
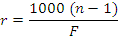
Putting the values to find r,
r = 1000 (1.523 – 1) / 12
Or, r = 1000 ( 0.523) / 12
Or, r = 523 / 12
Or, r = 43.58 mm
Therefore, we have
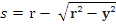
Or, s = 43.58 - √ 43.58² - 26 ²
Or, s = 43.58 - √ 1899.21 – 676
Or, s = 43.58 - √ 1223.21
Or, s = 43.58 – 34.97
Or, s = 8.61 mm
Therefore,
e = s + t
Or, e = 8.61 + 2
Or, e = 10.61 mm |
|
| |
Refractive Index of the lens material, Curve Variation Factor and Reflectance are important factors to be considered while selecting a suitable lens material for a lens prescription. They display light bending ability of a lens material, gives an approximate thickness comparison between two materials and also show the light transmissibility of the material. |
| |
Refractive Index |
Curve Variation Factor |
Reflectance |
Refractive Index of the lens material is the ratio between the velocities of the light in the air to the velocity of light in the lens material and is denoted by “n”. The number has no unit and is always greater than 1. Velocity of the light in the air is taken as 1,86,000 mile per second.
n = Velocity of light in Air / Velocity of light in the lens material
Application
Find the refractive index of crown glass, (if the velocity of light through it is 1,22,000 miles per second):
n = 1,86,000 / 1, 22,000
n = 1.52
Refractive index of crown glass = 1.52.
|
CVF shows the variation in lens surface power when the index of the lens material is changed from crown to other. It is a useful relationship to know the likely changes in the volume and lens thickness which will occur due to change in lens material.
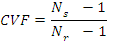
Where Ns is the Refractive Index of the standard lens material
Nr is the Refractive Index of the substituting lens material.
Application
What would be the change in lens surface power if the lens material is changed from crown to 1.70 white lenses?
1.523 - 1
CVF = ----------------
1.70 – 1
0.523
=----------
0.700
= 0.747 D
= 0.75 D approx. |
Reflectance is the loss of light transmission due to surface reflection. The loss of light transmission occurs at each of the lens surfaces. The reflectance of the lens surface is calculated from the refractive index of the material. When the light is normal on the lens surface, the percentage of light reflected at each surface is given by
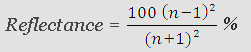
Therefore, a material of refractive index 1.5 has a reflectance of
100(1.5 – 1) ² / (1.5 + 1 )²
Or, 100 (0.5)² / (2.5)²
Or, 100 X (0.5 / 2.5)²
Or, 4 % per surface.
The higher the refractive index, the greater the proportion of light reflected from the surfaces. |
|
| |
Optician uses the term “Base Curve” to denote “the singular curve in the front side of the lens.” However, if two principle meridians of curvature are ground on the front side of the lens as it may be a case in case of toric lenses – the flatter of these two is referred as base curve, i.e, curve of the least power. Base Curve is a critical lens design factor to ensure a good balance between cosmetic appearance and good optics. Understanding Base Curve is the key to achieving Best Form and to minimize the lens aberration. |
| |
Spherical Equivalent |
Base Curve of the Ophthalmic Lens |
|
Spherical Equivalent for a sphero- cylinder lens prescription is the spherical power, the focal power of which coincides with the circle of least confusion. It is calculated by adding half of the cylinder element to the spherical power of the lens.
Example:
a) + 3.75sph –1.50cyl X 90 deg
Sph. Equivalent = + 3.00D
b) –3.00 sph–1.00cyl X 90deg.
Sph. Equivalent= -3.50D
|
Choosing an appropriate Base Curve , Rule of thumb is
For, Plus lens
Base Curve = Sph. Equivalent + 4.00
For, Minus lens
Base Curve= Sph. Equivalent + 8.00
Examples
1) + 3.75sph –1.50cyl X 90 deg
Sph. Equivalent = + 3.00D
Base Curve = + 3.00 +4.00 =
+ 7.00
2) –3.00 sph–1.00cyl X 90deg.
Sph. Equivalent= -3.50D
Base Curve = (- 3.50) + 8.00 =
+ 4.50
|
|
| |
|
| |
Vertex Distance Compensation Formula |
Keratometry Conversion Formula |
|
The vertex distance compensation formula is as under:
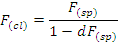
Where d stands for change in vertex distance in metres.
For example, a given spectacle refraction reads
– 7.00 / -1.00 X 180
Spherical Equivalent = (-7.00) + (-0.50) = -7.50D
Contact lens power after vertex correction will be:
F (cl) = - 7.50 / 1 – (+0.012) (-7.50)
= -6.88 Dsph
|
Keratometer gives radius of curvature in mm which may be converted into corneal dioptre by using following formula:
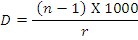
Where
r is radius of curvature in mm. and
n is the refractive index of cornea, which is taken as 1.3375
|
|
| |
|
| |
|
In case of plus lens, an increase in vertex distance increases the effective power of the lens, whereas in case of minus lens an increase in vertex distance will decrease the effective power of the lens.
The lens effectivity formula calculates the effective power of the lens when it is placed at a new distance. The equation is:
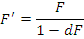
Where
F' = Effective Power of the lens at its new distance
F = Effective Power of the lens at its initial distance
d = Change in vertex distance in meters ( d is positive if the vertex distance increases and d is negative if vertex distance decreases)
Application:
What is the plus –add effect for a patient if he increases his -4.50 Dsph spectacle lens vertex distance by 10 mm?
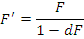
Or, = -4.50 / 1 – (+ 0.010)(-4.50)
Or, = -4.31 Dsph
The added plus effect is
-4.31 – (-4.50)
+0.19Dsph
|
| |
|
| |
Calculating Near Addition
Near Addition = Near Power – Distance Power
Application
Distance Power is – 2.50 Dsph and the Near Power is Plano, what is the Near Addition?
Near Addition = 0 – (- 2.50) = +2.50Dsph
Calculating Near Power
Near Power = Distance Power + Near Addition
Application
Distance Power is – 2.50 Dsph and the Near Addition is +2.00 Dsph, what is the Near Power?
Near Power = (-2.50 ) + (+2.00) = -0.50 Dsph. |
| |
| |
| |
| |
| |
|
|